01. What is a Matrix?
What is a Matrix?
Our next step is to understand what a Matrix is.
Before we dive into the video, let's cover a few necessary definitions and calculations!
So what is a Matrix? No, not that Matrix. The Matrix we are referring to was designed and created well before 1999.
A Matrix is a two dimensional array that contains the same elements as the vector.
A Matrix can have m rows and n columns.
If a Matrix has m rows and n columns is it called an m x n matrix.
Lets take a look at matrix A in the equation below:
A=\begin{bmatrix} a_{11} &a_{12} &a_{13}&..& a_{1n}\\ a_{21} &a_{22} &a_{23}&..& a_{2n}\\a_{31} &a_{32} &a_{33}&..& a_{3n}\\ :\\a_{m1} &a_{m2} &a_{m3}&……& a_{mn}\end{bmatrix}
Equation 11
Each element a_{ij} in the matrix displayed in equation 11 is a numerical value displayed in row i and column j.
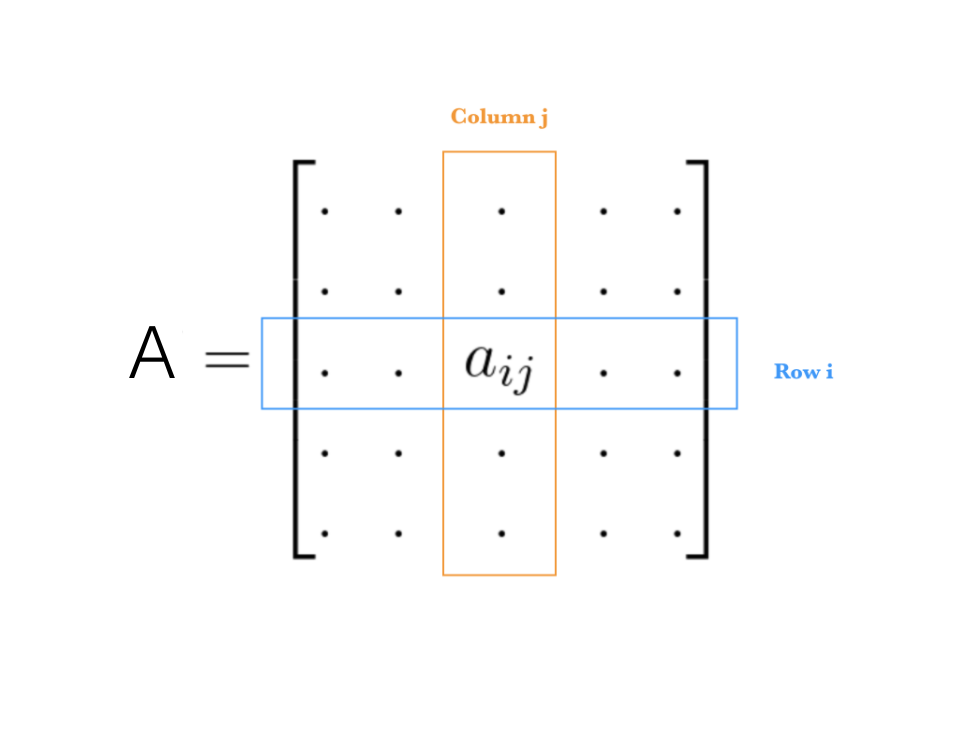
Element ij matrix A
Our next step is to understand how to apply matrix arithmetic: to perform operations such as:
- Matrix Addition
- Scalar multiplication of a matrix
- Matrix multiplication
When performing any mathematical calculations on matrices, we need to make sure we are working with the appropriate dimensions. We also need to be very careful with the indices.
Once we understand that, the rest becomes easier! Let's look at the details: